Mean

Arithmetic Mean

$Arithmetic Mean$

Geometric Mean

$Geometric Mean$

Harmonic Mean

$Harmonic Mean$

Mean of Probability Distribution

$Discrete Probability Mean$

$Continuous Probability Mean$

Mode

The mode of a sample is the element that occurs most often in the collection. For example, the mode of the sample [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] is 6.

Median

Standard Deviation and Variance

Variance

The variance of a random variable X is the expected value of the squared deviation from the mean of X:

Var(X) = E[(X - μ)²]

Usually the expected value for most distributions is the arithmetic mean:

$Variance with arithmetic mean$

Standard Deviation

Standard deviation is the square root of the variance.

Example

Example: The marks of a class of eight students (that is, a population) are the following eight values:

For example, the marks of a class of eight students (that is, a population) are the following eight values:

$2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9.$

These eight data points have the mean (average) of 5: ${\frac {2+4+4+4+5+5+7+9}{8}}=5.$

First, calculate the deviations of each data point from the mean, and square the result of each:

${\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16.\\end{array}}$

The variance is the mean of these values:

${\frac {9+1+1+1+0+0+4+16}{8}}=4.$

and the population standard deviation is equal to the square root of the variance:

${\sqrt {4}}=2.$

Normal Distribution

Probability Density

$Probability Density of a Normal Distribution$

Bessels Correction

Sample standard deviation

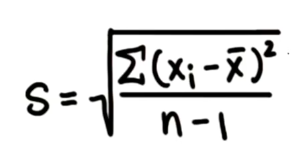
Bessels Correction

This is used to approximate standard deviation of the population, from a standar deviation of a sample.

Reference: Wikipedia