Dimensionality Reduction

Principal Component Analysis

Definition

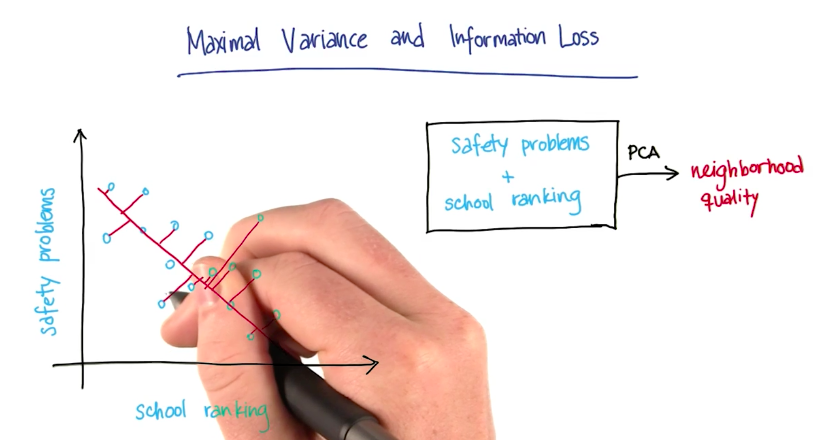
When to use PCA

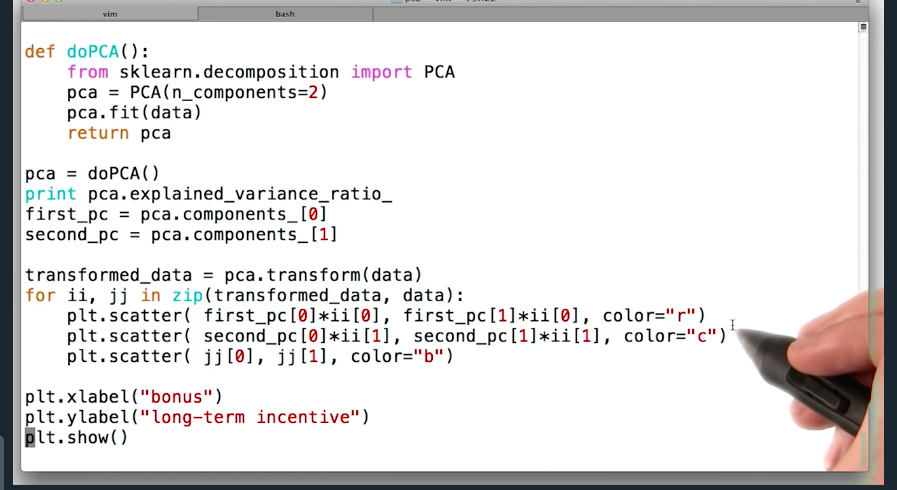
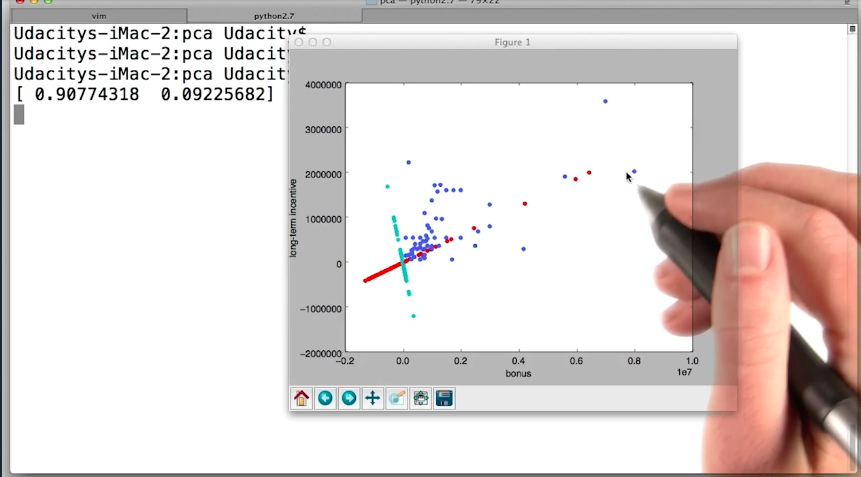
PCA in sklearn

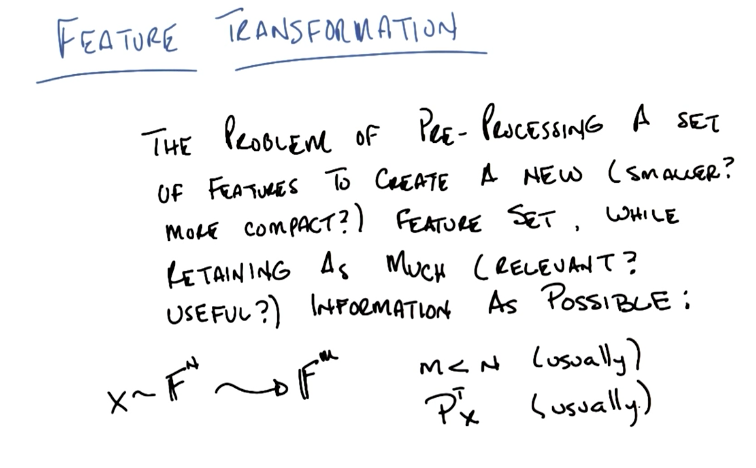
Feature Transformation

Definition

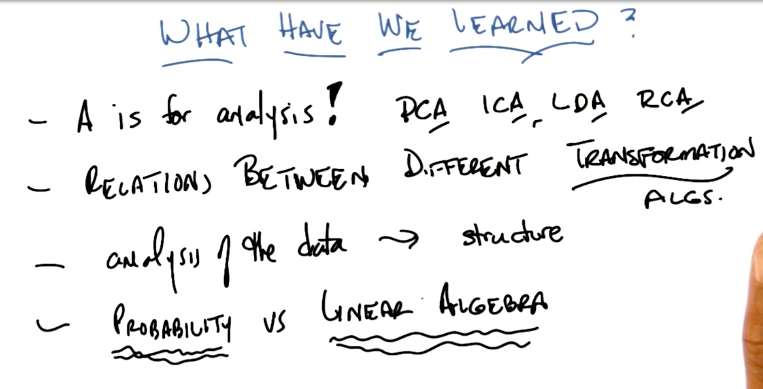
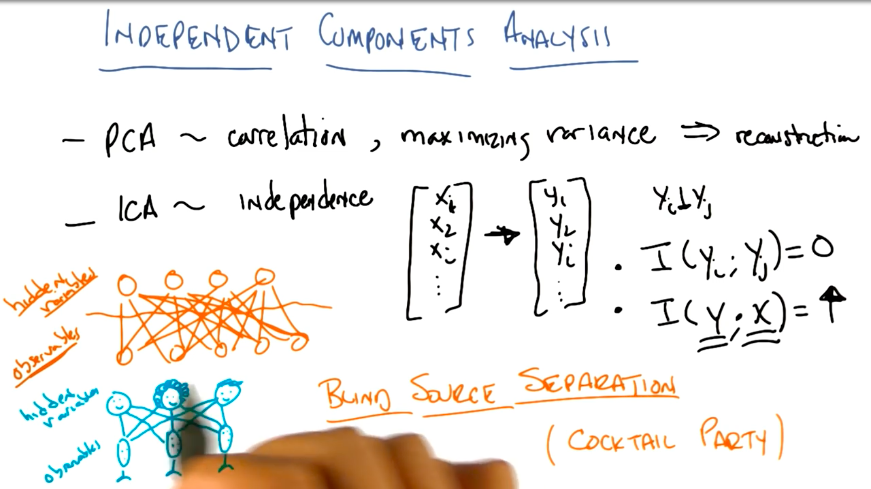
Independent Component Analysis

Independent component analysis (ICA) is a method in which the goal is to find a linear representation of nongaussian data so that the components are statistically independent, or as independent as possible. This paper describes ICA in detail. ICA has also been applied to the information retrieval problem, in a paper written by Charles himself.

The cocktail party demo is an example of ICA application

ICA vs PCA

• ICA:
  • finds hidden features
  • finds statistically independent features
  • maximizes mutual information
  • order between found features don’t matter
  • works better on nongaussian distributions
  • is a probabilistic analysis
• PCA:
  • decomposes the data onto orthogonal dimensions
  • maximizes variance
  • maximizes reconstruction
  • order between found features matters - former features cover more variance than latter features
  • works better on gaussian distributions
  • is a linear algebra analysis

In the image above:

• BSS stands for Blind Source Separation problem (ie: Cocktail Party).
• Directional means that ICA input direction is meaningful. For example, ICA will output two different results for a matrix M and M^T, while, PCA will output the same result for both inputs.
• Faces: PCA will find Brightness, then Average Face (eigenfaces), while ICA will find feature selectors like noses, mouths, eyes, etc.
• Natural Scenes: ICA will find edges.
• Documents: ICA will find topics.

Alternatives

• RCA: Random Component Analysis consists on projecting the data into random dimensions. It works in both cases, when M < N and also where M > N (for example: Kernel Methods)
• LDA: Linear Discriminant Analysis consists of using labels to find projections that summarize the data.

Summary

This excellent paper is a great resource for the Feature Transformation methods from this course, and beyond