machine-learning-nanodegree
Class notes for the Machine Learning Nanodegree at Udacity
Go to IndexArtificial Neural Networks
Perceptrons
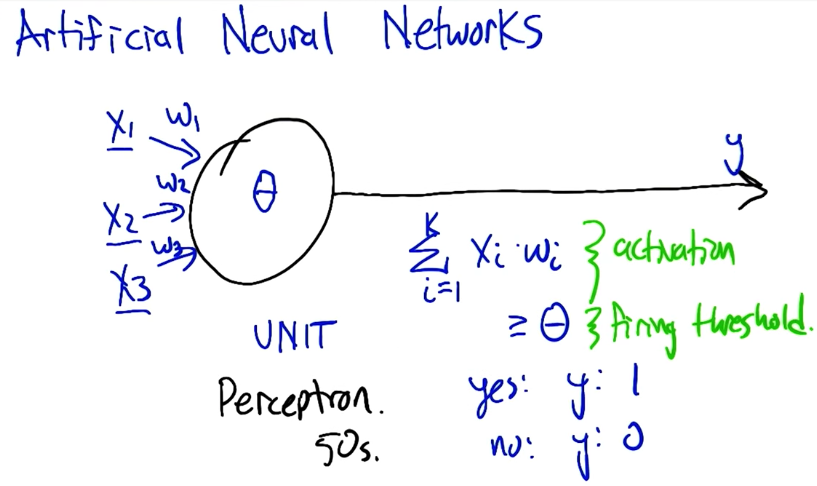
Boolean Operation Perceptrons
These perceptrons can be defined by the W and Θ values. Also note that there are multiple values of W and Θ that implement these operators.
AND
| X1 | X2 | W1 | W2 | Θ | Σ X*W | Y | AND |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 2 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 2 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 2 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
OR
| X1 | X2 | W1 | W2 | Θ | Σ X*W | Y | OR |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 |
NOT
| X1 | W1 | Θ | Σ X*W | Y | NOT |
|---|---|---|---|---|---|
| 0 | -1 | 0 | 0 | 1 | 1 |
| 1 | -1 | 0 | -1 | 0 | 0 |
XOR
| X1 | X2 | X3 (X1 AND X2) | W1 | W2 | W3 | Θ | Σ X*W | Y | XOR |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | -2 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | -2 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | -2 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | -2 | 1 | 0 | 0 | 0 |
Perceptron Training Rule
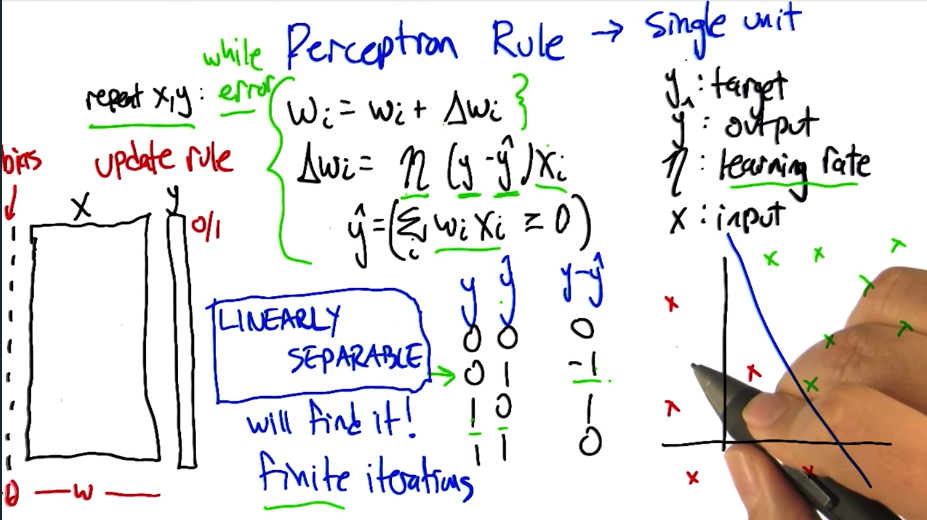
Gradient Descent Rule

Comparison of Learning Rules

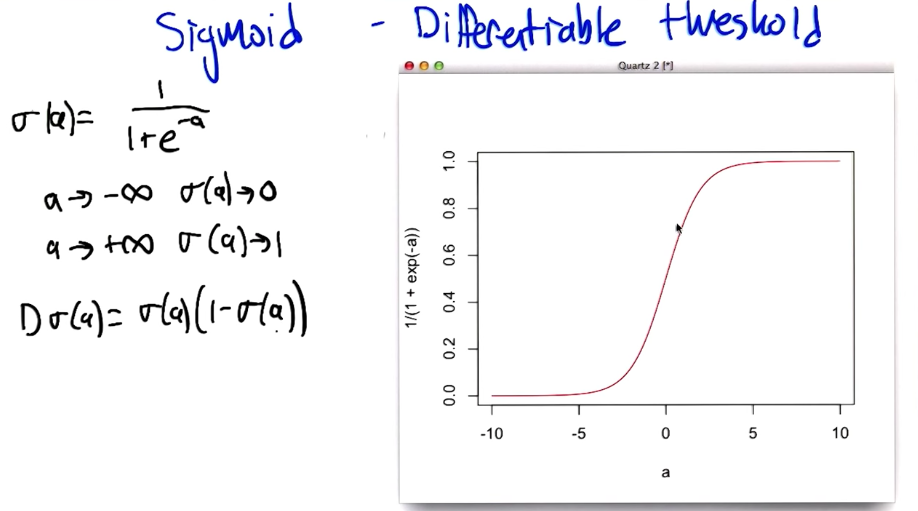
Sigmoid
Neural Network Sketch / Backpropagation
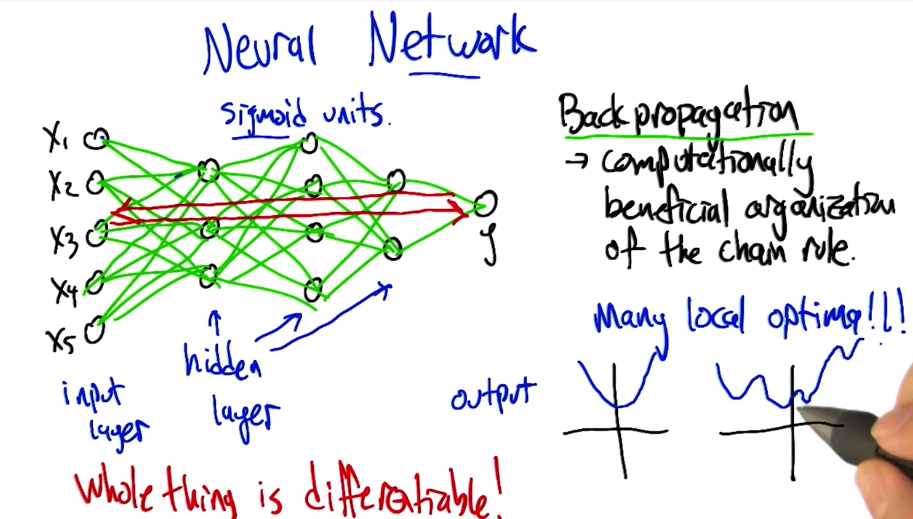
Optimizing Weights

Restriction Bias

Preference Bias

Summary
